Floating Point 부동소수점, Heap, Stack, Overflow

부동소수점 

컴퓨터에서 실수를 표시하는 방법으로, 소수점의 위치를 고정시키지 않으며 가수와 지수를 사용하여 실수를 표현한다. 가수는 유효숫자를 나타내며 지수는 소수점의 위치를 나타낸다.
부동 소수점은 (가수)X(밑수)(지수)와 같이 곱셈 형태로 표현하며, 밑수는 일반적으로 2나 10, 16을 사용한다. 실제 컴퓨터에서는 2진법을 사용하여 부호비트(1비트), 지수부, 가수부로 나타낸다. 소수점의 위치가 지수부의 크기에 따라 변경되며 소수점은 지수부와 가수부 사이에 있는 것으로 간주한다.

예를 들어 고정 소수점 0.1을 밑수가 10인 부동 소수점으로 표현하면 0.01X101이 된다. 가수의 첫째 자리를 밑수보다 작은 한 자리 자연수가 되도록 바꾸는 것을 정규화라고 하며, 위의 수를 정규화하면 1X10-1이다. 고정 소수점 0.4를 밑수가 2인 부동 소수점으로 표현하면 0.8X2-1이고 정규화하면 1.6X2-2이다.

부동 소수점은 기존의 고정 소수점 방식보다 아주 크거나 작은 수를 나타낼 수 있어, 과학 분야로 응용되어 사용된다. 또한 메모리의 효율성이 높으며 음수의 표현이 간단하지만, 하드웨어의 비용이 증가하고 고정 소수점 방식에 비해 연산 속도가 느리며 유효숫자인 가수의 자릿수가 정해져 있다.
출처 : 네이버 지식백과 / 두산백과 두피디아, 두산백과

 

---

 

https://ko.wikipedia.org/wiki/부동소수점

부동소수점 - 위키백과, 우리 모두의 백과사전

부동소수점(浮動小數點, floating point) 또는 떠돌이 소수점[1] 방식은 실수를 컴퓨터상에서 근사하여 표현할 때 소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적는 것으로, 유효숫자를 나타내는 가수(假數)와 소수점의 위치를 풀이하는 지수(指數)로 나누어 표현한다.

컴퓨터에서는 고정 소수점 방식보다 넓은 범위의 수를 나타낼 수 있어 과학기술 계산에 많이 이용되지만, 근삿값으로 표현되며[2] 고정 소수점 방식보다 연산 속도가 느리기 때문에 별도의 전용 연산 장치를 두는 경우가 많다. 고정 소수점과 달리 정수 부분과 소수 부분의 자릿수가 일정하지 않으나, 유효 숫자의 자릿수는 정해져 있다.

---

32비트 컴퓨터에서의 부동소수점 방식

실제 컴퓨터에서는 보통 이진법을 사용하여 다음과 같이 세 부분의 값으로 실수를 나타낸다.

부호부 (1비트) : 양수일 때는 0, 음수일 때는 1
지수부 (부호가 없는 정수, 8비트) : 8비트로 표시
정규화된 가수부 (부호가 없는 정수, 23비트) : 제일 앞의 비트는 정규화되었으므로 1이다.
예를 들어, 십진수 21.8125를 정규화된 이진수로 나타낸다고 해보자. 소수점 위의 (21.)10=(10101)2이고, 소수점 아래 (0.8125)10=(0.1101)2이다. 즉 (21.8125)10=(10101.1101)2이며, 이를 정규화하면 0.101011101×25이다. 지수의 5를 이진법으로 바꾸면 101이다. 따라서, 32비트 정규화된 부동소수점수로 나타낸다면 맨 앞 비트의 부호는 0(양)이고, 지수부 부호는 0(양)이며, 지수부 나머지 6개 비트는 000101, 가수부는 101011101000…이 된다. 이것을 결합하면 (00000010110101110100000000000000)2가 된다.[ref 2]

원리

부동 소수점 표현 방식은 수를 (가수)×(밑수)(지수)와 같이 유효숫자를 사용한 곱셈 형태로 표현한다. 예를 들어, -0.4를 밑수가 10인 부동 소수점으로 나타내면 -0.04×101이 되며 밑수가 2이면 -0.8×2-1가 되는데, 가수 부분을 한자리 자연수를 갖도록 바꾸면 -4×10-1과 같이 된다. 이처럼 가수의 첫째 자리가 밑수보다 작은 한자리 자연수가 되도록 바꾸는 것을 정규화라고 한다. 예를 들어, 앞의 값은 밑수가 2이면 -0.8×2-1이 되는데 이것을 정규화하면 -1.6×2-2이 된다. (여기서 볼 수 있듯이 밑수가 2일 때 정규화하면 가수부분의 첫째 숫자는 항상 1이 된다.)

컴퓨터 프로그래밍이나 전자계산기 등에서는 밑수가 10인 경우에 로마자 E 또는 e를 사용하여 함수 형태로 표시하기도 하는데, -0.4는 -0.04E+1 또는 -0.04e+1이 되며, 정규화하면 -4E-1 또는 -4e-1로 쓴다. 만약, 사용할 밑수를 미리 정해 놓는다면 가수와 지수만으로 실수를 표현할 수 있는데, 앞의 보기에서 밑수를 10으로 고정한다면 실수 -0.4는 가수 -4와 지수 -1의 조합으로 나타낼 수 있다. 보다 정형화된 형태로는 가수부와 지수부의 자릿수를 고정할 수 있는데, 만약 밑수는 10이고 부호는 따로 표시하며, 가수부 5자리, 지수부 3자리로 하는 형식이라면 앞의 값 -0.4는 '부호 -, 가수 40000, 지수 -005'로 나타낼 수 있다. 밑수가 2일 때에 정규화 결과 가수의 첫째 자리는 항상 1이 되므로 표시를 생략할 수 있다. 따라서, 고정된 형식에서 가수부에 1자리를 더 표시할 수 있게 되므로, 처리할 수 있는 유효숫자가 1자리만큼 늘어 난다. 앞의 예 1.6×2-2를 이 방식으로 표현하면 '부호 +, 가수 60000, 지수 -002'가 된다.

지수부에는 따로 부호 비트가 없기 때문에 음수 지수를 처리하기 위해 보통 바이어스 표현법을 사용한다. 즉, 할당된 자릿수로 표현 가능한 전체 영역을 반으로 나누어, 작은 영역에는 음수값 및 0, 큰 영역에는 양수값이 차례대로 1:1 대응되도록 한다. 예를 들어, 지수부를 8비트로 표현한다면 모두 256가지 수를 나타낼 수 있는데 이것을 반으로 나누어 음수 127개와 0, 양수 128개를 차례대로 대응시킨다. 따라서, 비트열 00000000은 지수 -127을 나타내고, 01111111은 지수 0, 11111111은 지수 128을 나타낸다. 일반적으로는 지수부가 n비트일 때 (2n / 2 - 1 = 2n-1 - 1)을 지수 값에 더하며 이것을 바이어스 상수라고 한다. (다만, 지수부의 모든 자리가 모두 0 또는 1인 경우는 각각 0 또는 무한대를 나타내는 등 종종 특수한 목적으로 예약되어 있다.) 가수부에서는 정규화 결과 유효숫자의 첫째 자리는 언제나 1이므로 표시하지 않고, 소수 부분만 표현한다.

---

정확도 문제

부동 소수점으로 표현한 수가 실수를 정확히 표현하지 못하고 부동 소수점 연산 역시 실제 수학적 연산을 정확히 표현하지 못하는 것은 여러 가지 문제를 낳는다.

예를 들어, 0.1과 0.01을 표현하지 못하므로 0.1의 제곱이 0.01이 되지도 않고 0.01과 가장 가까운 수가 되지도 않는다. 24비트 단정밀도 표현에서, 십진수 0.1은 지수 = -4; 가수 = 110011001100110011001101 이고 그 값은,
정확히 0.1000000014901161193847656256이다.
이 수를 다시 제곱하면,
정확히 0.010000000298023226097399174250313080847263336181640625이다.
단정밀도 부동 소수점 (반올림 있는) 하드웨어에서 제곱을 한다면,
정확히 0.010000000707805156707763671875이다.
하지만 0.01과 가장 가까운 표현 가능한 실수는
정확히 0.009999999776482582092285156250이다.
또한, π (및 π/2)를 표현하지 못하므로 tan(π/2)가 무한대의 값이 나오지 않으며 오버플로(overflow)가 생기지도 않는다. 따라서 π/2를 정확히 표현하지 못하기 때문에 일반적인 부동소수점 하드웨어에서는 tan(π/2)를 계산하는 일이 불가능하다. C 언어에서 아래의 계산 결과는 16331239353195370.0 가 된다.

double pi = 3.1415926535897932384626433832795;
double z = tan(pi/2.0);

단정밀도에서는 (tanf 함수를 이용하여), −22877332.0 라는 결과를 얻는다.

같은 이유로 sin(π)는 0이 되지 않고 배정밀도에서 약 0.1225×10-15 또는 단정밀도에서 −0.8742×10-7가 된다. [3]
부동소수점 덧셈과 곱셈은 모두 교환법칙 (a + b = b + a 이고 a × b = b × a)이 성립하지만, 꼭 결합법칙이 성립하지는 않는다. 즉, (a + b) + c 이 항상 a + (b + c) 과 같지는 않게 된다. 예를 들면 7자리 부동소수점(Float 7) 10진수 계산을 할 때:

1234.567 + 45.67846 = 1280.245
                      1280.245 + 0.0004 = 1280.245
그러나
45.67846 + 0.0004 = 45.67886
                    45.67886 + 1234.567 = 1280.246

또한 항상 분배법칙이 성립하지도 않는다. 즉, (a + b) × c 은 a × c + b × c과 다를 수 있다:

 

1234.567 × 3.333333 = 4115.223
1.234567 × 3.333333 = 4.115223
                      4115.223 + 4.115223 = 4119.338
그러나
1234.567 + 1.234567 = 1235.802
                      1235.802 × 3.333333 = 4119.340

유효 숫자를 잃어버리는 문제 뿐만 아니라, π와 0.1를 정확하게 표현하지 못하는 문제와 다른 약간의 부정확성이 다음과 같은 현상을 일으킨다:

- 소거: 거의 같은 두 값을 빼는 것은 정확성을 매우 많이 잃게 된다. 이 문제가 아마도 가장 일반적이고 심각한 정확도 문제이다.
- 정수로의 변환 문제: (63.0/9.0)을 정수로 변환하면 7이 되지만 (0.63/0.09)는 6이 된다. 이는 일반적으로 반올림 대신 버림을 하기 때문이다.
- 제한된 지수부: 결과값이 오버플로되어 무한대값이 되거나 언더플로되어 비정규 값 또는 0이 될 수 있다. 만약 비정규 값이 되면 유효숫자를 완전히 잃어버린다.
- 나눗셈이 안전한지 검사하는데 문제가 생김: 제수(나눗수)가 0이 아님을 검사하는 것이 나눗셈이 오버플로되고 무한대값이 되지 않는 걸 보장하지 않는다.
- 같음을 검사하는데 문제가 생김: 수학적으로 같은 계산결과가 나오는 두 계산 순서가 다른 부동소수점 값을 만들어낼 수 있다. 프로그래머는 어느정도의 허용 오차를 가지고 비교를 수행하지만, 그렇다고 해서 문제가 완전히 없어지지 않는다.

 

---

 

https://ko.wikipedia.org/wiki/스택_오버플로

스택 오버플로 - 위키백과, 우리 모두의 백과사전

Stack overflow
소프트웨어에서 스택 오버플로(영어: stack overflow)는 스택 포인터가 스택의 경계를 넘어설 때 일어난다. 호출 스택은 제한된 양의 주소 공간을 이루며 대개 프로그램 시작 시 결정된다.

프로그램이 호출 스택에서 이용 가능한 공간 이상을 사용하려고 시도할 때, 스택이 오버플로(overflow)된다고 하며 이 경우 일반적으로 프로그램 충돌이 발생하게 된다.[1]

무한 반복
스택 오버플로의 가장 흔한 원인은 상당히 깊거나 무한으로 이어지는 루프이다. 테일 콜 최적화 기능이 있는 스킴과 같은 언어들은 스택 오버플로 없이 특정한 정렬인 테일 반복으로 무한 반복을 일으키게 한다. 이는 테일 콜이 추가적인 스택 공간을 차지하지 않기 때문에 가능하다.[2]

C의 무한 루프의 예는 다음과 같다.

int foo() {
     return foo();
}

foo 함수가 발생되면 자신을 호출하여 스택 오버플로가 일어날 때까지 매번 스택에 추가 공간을 사용하며 결국 세그멘테이션 오류가 발생한다.[3]

 

---

https://ko.wikipedia.org/wiki/힙_오버플로

힙 오버플로 - 위키백과, 우리 모두의 백과사전

Heap overflow
힙 오버플로(heap overflow)는 힙 데이터 영역에서 발생하는 버퍼 오버플로의 한 종류이다. 힙 오버플로는 스택 기반 오버플로와는 다른 방식으로 익스플로잇 가능하다. 힙에서의 메모리는 런타임 시에 애플리케이션에 의해 동적으로 할당되며 일반적으로 프로그램 데이터를 포함한다. 익스플로잇은 애플리케이션이 링크드 리스트 포인터 같은 내부 구조체를 겹쳐쓰는 것 같이 이 데이터를 특정한 방식으로 오염시킴으로써 수행된다. 고전적인 힙 오버플로 기법은 동적 메모리 할당 연결(malloc 메타 데이터 같은)을 겹쳐쓰고 프로그램 함수 포인터를 겹쳐쓰기 위해 결과로 나온 포인터를 교환하는 기법이다.

옛날 버전의 리눅스에서의 전형적인 예시는 힙에서 두 버퍼가 각각 나란히 할당되고, 첫 번째 버퍼의 경계 외부에 쓰는 것이 두 번째 버퍼의 메타 데이터를 겹쳐쓰게되는 것이다. 두 번째 버퍼의 사용 비트를 0으로 설정하고 널 바이트들이 복사되게 하기 위해 작은 음수 값을 길이로 설정한 후에, 첫 번째 버퍼에서 프로그램이 free() 함수를 호출할 때 프로그램은 이 두 버퍼를 단일 버퍼로 통합하려는 시도를 할 것이다. 이 상황이 벌어지면 free될 버퍼는 이전에 할당된 버퍼의 첫 8 바이트에 포워드와 백이라는 두 포인터를 갖게 된다.

결과
우연한 오버플로는 영향을 받은 메모리 영역을 사용하는 프로세스들에서 데이터 오염이나 예상치 못한 행위를 야기한다. 메모리 보호가 없는 운영 체제에서 이것은 시스템의 어느 프로세스라도 가능하다.
의도적인 익스플로잇은 데이터가 특정한 영역에서 임의적인 방식으로 바뀌거나 임의적인 코드를 실행되게 하는 것을 야기한다.
예를 들면 마이크로소프트 JPEG GDI+ 버퍼 오버플로 취약점은 감염된 머신에서 코드의 원격 실행을 허용한다.[1]
iOS 탈옥은 임의 코드 실행을 위해 종종 힙 오버플로를 사용하는데 이것은 보통 커널을 탈옥한 것으로 교체하기 위해 커널 익스플로잇을 위한 것이다.

탐지와 방어
힙 오버플로를 방어하는 방식으로 세 종류가 있다. 여러 현대 운영 체제들은 세가지 모두의 구현 중 일부를 제공한다.
일반적으로 NX 비트 같은 하드웨어 특징들을 통해 코드와 데이터를 분리함으로써 페이로드의 실행을 막는다
힙이 고정된 오프셋에서 발견되지 못하게 난수화를 도입한다
힙 매니저에 대한 분별력 있는 검사를 도입한다.
GNU libc는 2.3.6 버전부터 unlink를 호출할 때 포인터의 일관성을 검사하는 것 같이 힙 오버플로를 탐지하는 방어가 포함되었다. 그러나 이러한 방어들은 거의 즉시 공격 가능하다고 밝혀졌다.[2][3] 추가적으로 리눅스는 (비록 PaX가 몇 년 전에 더 나은 구현을 도입하였지만) 2005년 이후부터는 ASLR을 포함하였다. 또한 리눅스는 2004년부터는 NX 비트의 지원을 포함하였다.
마이크로소프트는 2003년부터 힙에 기반한 버퍼 오버플로에 대한 방어를 포함하였다. 이러한 완화는 안전한 링크해제와 힙 엔트리 헤더 쿠키가 있다. 윈도우의 최근 버전들은 일반적으로 대상이 되는 데이터 구조체들의 제거, 힙 엔트리 메타데이터 난수화, 함수 포인터 인코딩, 힙 오염의 종료 그리고 알고리즘 변이를 포함한다. 일반 데이터 실행 방어(DEP)와 ASLR 도 또한 이 공격을 완화시키는데 도움을 준다.[4]

 

---

 

https://ko.wikipedia.org/wiki/스택

스택 - 위키백과, 우리 모두의 백과사전

Stack
스택(stack)은 제한적으로 접근할 수 있는 나열 구조이다. 그 접근 방법은 언제나 목록의 끝에서만 일어난다. 끝먼저내기 목록(Pushdown list)이라고도 한다.

스택은 한 쪽 끝에서만 자료를 넣거나 뺄 수 있는 선형 구조(LIFO - Last In First Out)으로 되어 있다. 자료를 넣는 것을 '밀어넣는다' 하여 푸쉬(push)라고 하고 반대로 넣어둔 자료를 꺼내는 것을 팝(pop)이라고 하는데, 이때 꺼내지는 자료는 가장 최근에 푸쉬한 자료부터 나오게 된다. 이처럼 나중에 넣은 값이 먼저 나오는 것을 LIFO 구조라고 한다.

이를테면, a부터 b와 c를 순서대로 넣은 다음 자료를 하나씩 꺼내면 c부터 b와 a의 순서로 나오게 된다. S를 스택, x를 데이터 요소(element)라고 하자. 그러면 스택에서는 아래와 같은 중요한 연산이 존재하는 것을 알 수 있다.

S.top(): 스택의 가장 윗 데이터를 반환한다. 만약 스택이 비었다면 이 연산은 정의불가 상태이다.
S.pop(): 스택의 가장 윗 데이터를 삭제한다. 스택이 비었다면 연산 정의불가 상태.
S.push(): 스택의 가장 윗 데이터로 top이 가리키는 자리 위에(top = top + 1) 메모리를 생성, 데이터 x를 넣는다.
S.empty(): 스택이 비었다면 1을 반환하고,그렇지 않다면 0을 반환한다.
또한, 스택연산을 목록(list) 연산으로 표현할 수도 있다.

S.top(): S.retrieve(S.first())
S.pop(): S.top(),S.delete(S.first())
S.push():S.insert(x,pNull)
S.empty():S.first()==pNull
컴퓨터에서 포인터라고 하는 자료의 위치 표시자와 넣고 빼는 명령어를 사용해서 스택을 이용한다. 주로 함수를 호출할 때 인수의 전달 등에 이용된다. LIFO의 특징을 이용하여 역폴란드 표기법을 이용한 프로그래밍 언어인 포스(Forth) 등에서도 이용된다.

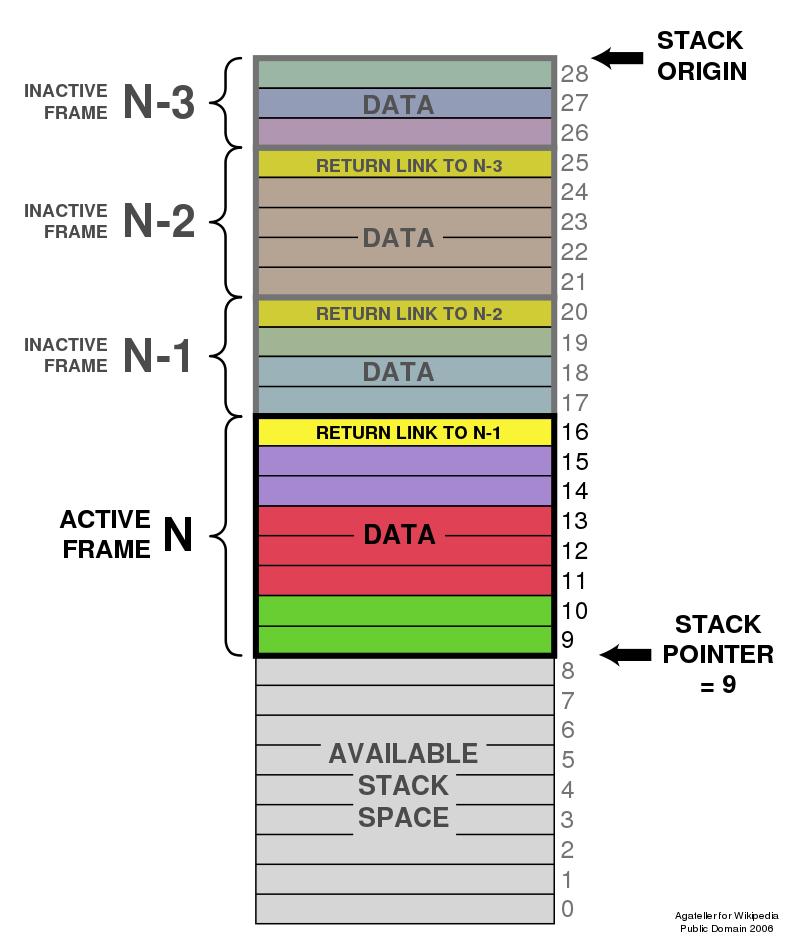
하드웨어 스택

아키텍처 수준에서 스택을 사용하는 것은 메모리의 할당 및 접근 수단을 의미한다.

 

---

 

https://ko.wikipedia.org/wiki/힙_(자료_구조) 

힙 (자료 구조) - 위키백과, 우리 모두의 백과사전

 

Heap

힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(complete binary tree)를 기본으로 한 자료구조(tree-based structure)로서 다음과 같은 힙 속성(property)을 만족한다.

 

A가 B의 부모노드(parent node) 이면, A의 키(key)값과 B의 키값 사이에는 대소관계가 성립한다.
힙에는 두가지 종류가 있으며, 부모노드의 키값이 자식노드의 키 값보다 항상 큰 힙을 '최대 힙', 부모노드의 키 값이 자식노드의 키 값보다 항상 작은 힙을 '최소 힙'이라고 부른다.

 

키 값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 특히 형제 사이에는 대소관계가 정해지지 않는다.
각 노드의 자식노드의 최대개수는 힙의 종류에 따라 다르지만, 대부분의 경우는 자식노드의 개수가 최대 2개인 이진 힙(binary heap)을 사용한다.
힙에서는 가장 높은(혹은 가장 낮은) 우선순위를 가지는 노드가 항상 뿌리노드에 오게 되는 특징이 있으며, 이를 응용하면 우선순위 큐와 같은 추상적 자료형을 구현할 수 있다.

이진 힙
이진 힙은 내부노드(internal node)에 키(key)와 요소(element)를 저장한 이진 트리로 다음과 같은 두 가지 특징을 갖는 것을 말한다.

트리를 T, 임의 내부노드를 v 라고 하면 다음과 같다:
1. 뿌리노드를 제외한 각 내부노드는 key(T.parent(v)) < key(v) 또는 key(T.parent(v)) > key(v)이다. (즉, 키 값은 오름차순이거나 내림차순이다.)
2. 마지막 왼쪽 결합 노드들의 레벨을 제외한 다른 모든 레벨들은 완전 이진트리를 형성한다.[1]

 

힙 리스트(heap list)로 표현할 때 i번째 노드의 왼쪽 자식노드의 위치는 2i가 되며, i번째 노드의 오른쪽 자식노드의 위치는 2i+1이고, 또한 i번째 노드의 부모노드의 위치는 i/2가 된다.

복잡도

예제
다음의 내용의 배열을 최대힙으로 구성하는 과정을 보여준다. [H|E|A|P|S|O|R|T]
이 배열을 사전 순서에 따라 (즉, A<B<C<…<Y<Z) 힙으로 구성하는 과정은 다음과 같다.

1 2 3 4 5 6 7 8
H E A P S O R T     //중간지점인 p(4번째 인덱스)에서 시작
      ^       ^     //그의 자식은 (왼쪽 자노드 인덱스8)T>P이기 때문에 교환
H E A T S O R P     //A(3번째 인덱스)로 계속되며 A의 왼쪽 자노드는 O(6번째 인덱스)가 되며 오른쪽 자노드는
    ^     ^ ^       //R(7번째 인덱스값)이 되는데 R>O,R>A이므로 R,A교환
H E R T S O A P     //E(인덱스 2)와 그 왼쪽 자노드T(인덱스 4),오른쪽 자노드S(인덱스 5)비교
  ^   ^ ^           //T>S,T>E 결국 T,E교환
H T R E S O A P     //계속 E(인덱스 4)는 왼쪽 자노드P(인덱스 8)과 비교교환하는데 P>E
      ^       ^
H T R P S O A E     //H(인덱스 1)은 그의 왼쪽 자노드T(인덱스 2)와 오른쪽 자노드R(인덱스 3)
^ ^ ^               //T>R,T>H비교 교환한다.
T H R P S O A E     //계속 H를 비교 교환하게 되는데,H(인덱스 2)이므로 왼쪽 자노드P(인덱스 4),오른쪽 자노드
  ^   ^ ^           //S(인덱스5)에서 S>P,S>H비교 교환하게 된다.
T S R P H O A E     //힙 구성 끝.

힙 구성 결과, 뿌리노드인 T는 그 자식노드인 S, R과 비교할 때 T>S, T>R의 관계를 가지며, 동일한 관계가 모든 노드와 그 자식노드에 대해 성립함을 볼 수 있다.

 

---