
Square root 제곱근
수학에서, 어떤 수의 제곱근(제곱根,자승근, 영어: square root)은 제곱하여 그 수가 되는 수를 가리킨다. 실수의 범위에서만 보면, 모든 양의 실수는 서로 덧셈 역원인 두 제곱근을 가지며, 이 중 음이 아닌 하나를 주요 제곱근(主要제곱根, 영어: principal square root)이라고 한다. 그러나 0의 제곱근은 0뿐이므로 이를 주요 제곱근으로 삼으며, 음의 실수의 실수 제곱근은 존재하지 않으므로 주요 제곱근을 정의할 수 없다. 예를 들어, 실수 9의 제곱근은 ±3이며, 이 중 주요 제곱근은 3이다. 또한 −4의 제곱근은 존재하지 않는다. 복소수의 범위에서 보면, 모든 0이 아닌 복소수는 서로 중심 대칭인 두 제곱근을 가지며, 이 중 편각이 원래의 반인 하나를 주요 제곱근으로 삼는다....
https://ko.wikipedia.org/wiki/%EC%A0%9C%EA%B3%B1%EA%B7%BC
제곱근 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 수학에서, 어떤 수의 제곱근(제곱根,자승근, 영어: square root)은 제곱하여 그 수가 되는 수를 가리킨다. 실수의 범위에서만 보면, 모든 양의 실수는 서로 덧셈 역
ko.wikipedia.org
https://ko.wikipedia.org/wiki/%EA%B7%BC_(%EC%88%98%ED%95%99)
근 (수학) - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 근(根)은 등식의 일종인 방정식에서 쓰이는 용어로, 특정한 문자에 대한 방정식에서 “특정한 문자”가 ‘어떤 값’으로 변하여 참을 만족했을 때, 그 ‘어떤
ko.wikipedia.org
두 점 사이의 직선 거리
좌표평면 상에서 두 점 사이의 거리를 구하는 공식이다.
피타고라스의 원리를 이용하면 쉽게 유도할 수 있다.
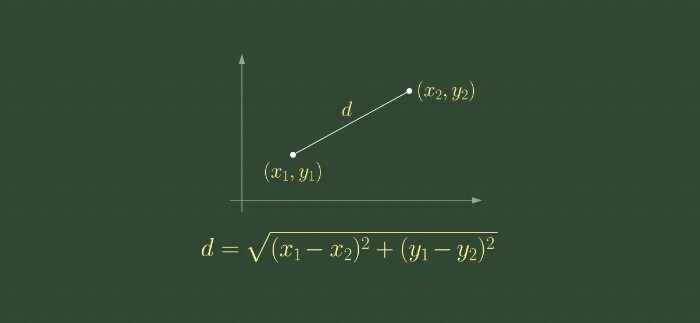
https://terms.naver.com/entry.naver?docId=3350310&cid=60210&categoryId=60210
Vector 벡터
물리학에서의 벡터는 시점 A에서 종점 P로 가는 유향선분 AP 또는 (AP위에 오른쪽으로 향한 화살표)로 표시된다. 이 같은 벡터가 1, 2, 3차원 공간에 있을 때, 그것은 원점 O에서 시작되고 길이와 방향이 각각 같은 벡터로 간주된다. 그러므로 이 같은 공간에서 원점 O를 시점으로 가지는 벡터만을 생각하기로 한다.
그런데 벡터 OP는 종점 P로 나타낼 수 있고, 반대로 어떤 점 P가 주어지면 한 벡터 OP가 존재한다. 그러므로 벡터 OP를 나타내는 데 P의 좌표 (x), (x, y), (x, y, z)를 쓸 수 있다. 즉, 1차원, 2차원, 3차원의 벡터는 각각 (x), (x, y), (x, y, z) 꼴로 나타난다. 이와 같이 생각하여, n차원 유클리드공간의 한 점
(x1, x2, ···, xn), xi는 실수,
을 n차원 벡터라 부르기로 한다.

벡터의 합을 정의하는 데 위의 그림에서와 같은(그림 이상한데..) 평행사변형의 법칙을 일반화하여 사용한다. 즉,
(x1, x2, ···, xn) + (x1', x2', ···, xn')
= (x1 + x1', x2 + x2', ···, xn + xn')
이라 정한다. 덧셈에 관하여 교환법칙과 결합법칙이 성립한다.
또, 원점(0, 0, ···, 0)을 영 벡터라 부르며, 한 벡터와 영 벡터의 합은 그 벡터 자신이 된다.
물리학에서는 시간, 질량, 온도, 에네르기 등의 양을 스칼라(scalar)라 부르는데, 이들은 실수로 나타난다. 그래서 실수를 스칼라라고도 부른다.
실수 a와 벡터의 곱은
a(x1, x2, ···, xn) = (ax1, ax2, ···, axn)
으로 정한다. a가 -1일 때
-(x1, x2, ···, xn) = (-x1, -x2, ···, -xn)
이라 정함으로써, 벡터와 벡터 사이의 뺄셈도 생각할 수 있다.
(수학의 세계, 2006. 9. 10., 박세희)
https://terms.naver.com/entry.naver?docId=2426084&cid=60208&categoryId=60208
기호가 너무 많음. 링크 들어가서 보자
벡터의 덧셈과 뺄셈
https://terms.naver.com/entry.naver?docId=2073864&cid=47324&categoryId=47324
벡터의 덧셈과 뺄셈
[ 1. 교과서 속 주개념] [ 1) 벡터의 덧셈] (1) 삼각형법 라 할 때, 삼각형의 변 를 와 의 합이라 하고 로 표현한다. (2) 평행사변형법 라 하고 와 를 두 변으로 하는 평행사변형OACB를 만들 때, 이므로
terms.naver.com
스칼라곱
https://terms.naver.com/entry.naver?docId=592150&cid=42340&categoryId=42340
스칼라곱
두 벡터양 A와 B가 있어서, 그 크기를 각각 A, B, 그 사이의 각을 θ라고 하면, 스칼라 곱은 다음 식과 같은 스칼라양이 된다. A · B=(A, B)=B · A=AB cosθ, 이 관계에서 A⊥B이면 A · B=0, A//B이면 A · B=AB
terms.naver.com
너무 어려운데 이해하고 싶은 단어들이 많다
컴퓨터에서의 수 표현 - 나무위키
일반적으로 컴퓨터에서 사용되는 정수형의 종류는 다음과 같다. 형크기char8비트short16비트int32비트long64비트 각 정수는 음수를 표현할 수 없고 양수 크기가 두 배로 지원되는 unsigned 형을 가진다.
namu.wiki
